Learning Moves – Rubik’s-Cube-Solver mit Memory-Effekt
Learning Moves ist ein lernfähiges Skript zur Lösung des Rubik’s Cube, das auf einem erweiterten Random-Solve-Ansatz basiert. Es merkt sich Zugfolgen, die den Zustand des Cubes verbessern, und speichert sie positionsbasiert. Bei jeder neuen Iteration prüft das Skript zuerst, ob für die aktuelle Position bereits eine bekannte Verbesserung existiert – und wendet diese direkt an. So entsteht ein wachsendes Repertoire an effektiven Teilstrategien. Mit jeder Runde wird Learning Moves dadurch effizienter und ersetzt zufällige Suche zunehmend durch gezieltes, erfahrungsbasiertes Handeln.
Skript Beschreibung
Learning Moves ist ein Python-Skript zur iterativen Lösung des Rubik’s Cube, das auf einem explorativen Random-Solve-Ansatz basiert – jedoch mit einem entscheidenden Unterschied: Das Skript ist in der Lage, aus erfolgreichen Zügen zu lernen und dieses Wissen bei späteren Versuchen gezielt anzuwenden. Es kombiniert brute-force-artige Zufallsstrategien mit einem persistenten Gedächtnis, das effektive Zugfolgen speichert und wiederverwendet.
Grundprinzip
Der Lösungsprozess besteht aus drei Phasen, die den klassischen Layer-by-Layer-Ansatz widerspiegeln:
- E1: Weißes Kreuz + weiße Ecken (Grundlagen)
- E2: Mittelsteine der zweiten Ebene (Kanten)
- E3: Gelbe Ebene (komplette Lösung)
Für jede Stufe versucht das Skript, eine zufällige Folge gültiger Züge zu finden, die zu einem besseren Zwischenzustand führt. Dabei wird der Fortschritt anhand der korrekt platzierten Steine (Pieces) gemessen. Diese werden präzise durch eine Definition von Farbkombinationen an festen Sticker-Positionen überprüft.
Lernmechanismus
Sobald eine Zugfolge gefunden wird, die den Zustand des Cubes verbessert (z. B. von 4 auf 6 korrekte Steine), wird diese zusammen mit dem Ausgangszustand in einer CSV-Datei gespeichert (Improvements.csv). Dabei gilt:
Jede Verbesserung wird nur einmal gespeichert (Duplikatprüfung über Start-Zustand + Zugfolge)
Zusätzlich wird ein Bewertungswert gespeichert, basierend auf dem Verhältnis von Verbesserung zu Zuglänge (Effizienzmaß)
Bei zukünftigen Durchläufen prüft das Skript für jede neue Ausgangsposition, ob bereits eine gespeicherte Verbesserung existiert. Wenn ja, wird die zugehörige Zugfolge direkt angewendet – ohne erneutes Herumprobieren. Dieser „Memory-Effekt“ führt dazu, dass der Solver über Zeit immer weniger zufällige Versuche braucht und zunehmend gezielter agiert.
Technische Details
Das Skript verteilt die Generierung von Kandidatenzugfolgen auf mehrere CPU-Kerne mithilfe von ProcessPoolExecutor, um die Performance bei der Suche nach Verbesserungen zu steigern. Alle relevanten Parameter wie maximale Iterationen, Zuglängen oder Zielwerte für korrekt platzierte Steine werden aus einer externen CSV-Datei geladen, wodurch sich das Verhalten des Skripts flexibel anpassen lässt. Die erzeugten Zugfolgen berücksichtigen sowohl inverse Züge als auch die potenzielle Beeinträchtigung bereits korrekt platzierter Teile, um destruktive Züge zu minimieren. Vor Beginn der eigentlichen Optimierung kann der Cube optional durch eine definierte Anzahl zufälliger Züge verdreht werden. Während des gesamten Ablaufs wird zudem protokolliert, wie häufig bereits gelernte Zugfolgen erfolgreich wiederverwendet wurden – eine Kennzahl für die Effektivität des Lernprozesses.
Dateistruktur
Improvements.csv: Langzeitgedächtnis für erfolgreiche Zugfolgen
Results.csv: Statistiken über jeden Run
csv_export-StartPos.csv: Eingabepositionen des Cubes
mappings.json: Definition der Permutationswirkung jedes Zugs
Ergebnisse
Während der verschiedenen Trainingsphasen ließ sich sehr deutlich beobachten, wie Learning Moves durch die Anwendung bereits gelernter Zugfolgen zunehmend effizienter wurde. Verbesserungen wurden schneller erkannt, die Lösungsschritte griffen gezielter – und die durchschnittliche Anzahl an Iterationen bis zum nächsten Fortschritt nahm spürbar ab. In vielen Fällen führten bekannte Zugfolgen bereits unmittelbar zur Zielkonfiguration eines Levels.
Statt sofort auf eine vollständige Lösung hinzuarbeiten, wurde das Skript zunächst schrittweise trainiert: Zuerst auf das Erreichen von 12 korrekten Steinen, dann 14, 16, 18 und schließlich 20. Dieses gestufte Lernverfahren erwies sich als sehr effektiv.
Ein wesentlicher Faktor für den Erfolg war die Wahl geeigneter Parameter. Manche Konfigurationen führten dazu, dass über Stunden hinweg keinerlei Fortschritt verzeichnet oder neue Zugfolgen gespeichert wurden. Besonders hilfreich war die Erkenntnis, dass sich kürzere, häufigere Abläufe mit weniger Iterationen pro Durchlauf als deutlich produktiver erwiesen haben. In der derzeit besten Parametervariante erreicht das Skript rund 50.000 Durchläufe pro Tag – mit über 1.000 vollständigen Lösungen im bisherigen Verlauf.
Learning Moves hat sich damit zu einem System entwickelt, das durch einfaches Wiederverwenden erfolgreicher Zugfolgen zunehmend effizienter arbeitet. Es kombiniert exploratives Verhalten mit einem wachsenden Erfahrungsschatz – und erzielt dabei bereits reproduzierbar gute Resultate. Auch wenn noch nicht alle Potenziale ausgeschöpft sind, zeigt sich bereits, dass dieser Ansatz eine solide Grundlage für weiterführende Optimierungen bietet.
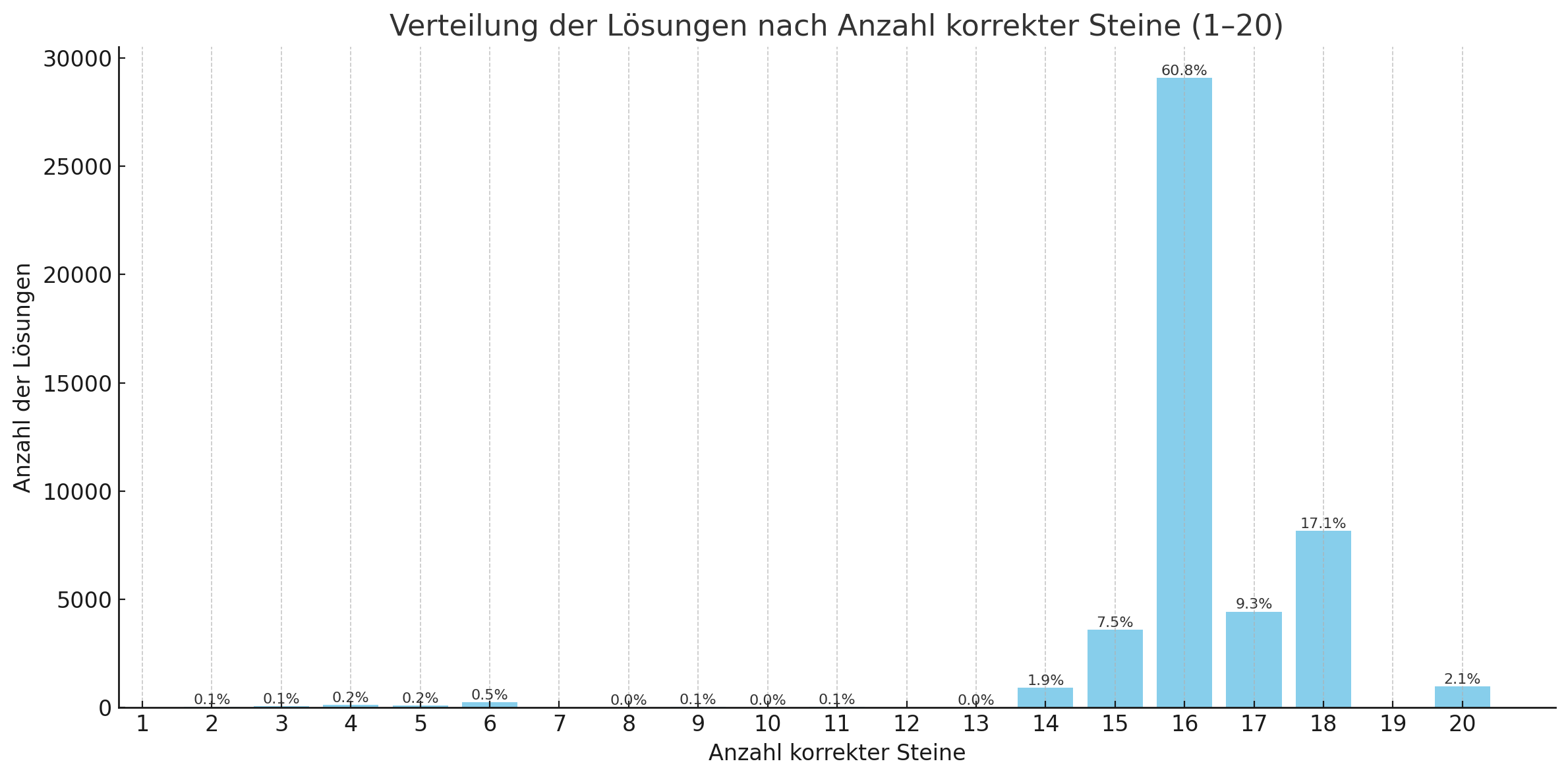
Die Grafik zeigt ziemlich klar, wie sich die Lösungen im Training von Learning Moves auf die Anzahl korrekt platzierter Steine verteilen. Besonders interessant: Etwa 2 % aller Versuche führten zu einer vollständigen Lösung mit 20 korrekten Steinen. Und das, obwohl das Skript in dieser Version noch keinen Mechanismus hatte, um in einer Sackgasse zurückzugehen oder einen Durchlauf frühzeitig abzubrechen.
Wenn das Skript z. B. 18 korrekte Positionen erreicht hatte, versuchte es einfach stumpf, den Rest in einem Rutsch zu lösen – mit eher kurzen, zufällig erzeugten Zugfolgen. Dass dabei trotzdem vollständige Lösungen herauskamen, zeigt, wie viel schon allein durch das Wiederverwenden gelernter Zugfolgen erreicht werden kann.
In der nächsten Version soll genau an dieser Stelle angesetzt werden: mit intelligenterem Zurückspringen, besseren Kombinationen und einer gezielteren Anwendung von bereits bekannten Teilstrategien. Da ist also noch einiges an Potenzial drin.
Auch wenn das Skript in der Lage war, rund 1.000 vollständige Lösungen zu erzeugen, ist beim Blick auf die Zuglängen klar: In Richtung Gottes Zahl – also der minimal möglichen Zuganzahl von 20 im HTM – ist es noch ein weiter Weg. Der Durchschnitt lag bei 92 Zügen, der kürzeste gefundene Lösungsweg bei 55, der längste bei 128. Das zeigt: Die aktuellen Lösungen sind noch stark geprägt von zufälligen und ineffizienten Zugfolgen, auch wenn sie zum Ziel führen. Der Fokus lag bisher auf dem ob, nicht dem wie effizient.
Ressourcen
Notwendig für die Skriptausführung
- Skript_02: LearningMoves.py
- Parameterdatei: parameter_csv-Parameter.csv
- Mappingdatei der Züge: mappings.json
- Importdatei mit Startposition: csv_export-StartPos.csv
Optional
- Datei mit den gelernten Zügen - wird vom Skript angelegt, wenn nicht vorhanden: Improvements.csv
- Skript zur Erstellung Startposition: CreateStartPosition.py
- Testskript zur Verifikation der Lösung: TestMoves.py